추정과 검정

추정과 검정은 굉장히 비슷하게 느껴지는 개념입니다.

먼저, 추정은 표본으로 부터 모수 또는 모수가 속한 구간을 구하는 것입니다. 검정은 모수에 대한 가정을 먼저 세우고, 그 가정에 대한 판단이 중점이 되는 것입니다.

앞선 포스팅의 Posteriori와 Likelihood를 생각해보면 좀 더 이해하기 쉬울 수 있습니다. 데이터를 두고 모수를 구하는 것은 추정. 모수를 두고 데이터와 정합성을 판단하는 것은 검정.

단일 모평균의 추정 및 검정

단일 모평균의 추정은 모집단의 평균으로 예상되는 값을 뽑아내거나, 모집단의 평균이 있을 법한 구간을 구하는 것이고, 단일 모평균에 대한 검정은 모집단의 평균을 특정한 값으로 가정한 뒤에 확률적으로 얼마나 말이 되는지 살펴보는 것입니다.

중심 극한 정리에 의해 표본의 평균은 평균과 분산을 변수로 가지는 정규분포를 따르게 된다고 말할 수 있지요.

모집단의 평균을 구하고 싶은 것이니, 자연스럽게 2가지로 나눠볼 수 있을 것입니다. 모분산을 알고 있는 경우, 그리고 모르는 경우!

모분산을 알고 있을 때 단일 모평균의 추정 및 검정

먼저, 추정에 대해 말하기 전에, 불편 추정량에 대해서 복습 겸 간단히 설명하겠습니다.

불편추정량이란 기댓값이 추정하고자 하는 모집단의 모수와 동일해지는 확률변수에 표본을 대입한 값입니다.

평균 \(\mu\) 를 가지는 모집단에서 표본 n개를 뽑았을 때. 표본평균은 모평균의 불편 추정량입니다.

이를 간단히 증명해보면,

\(\begin{aligned} E[\bar{X}] = E[\frac{1}{n}\sum X_i] = \frac{1}{n}\sum E[X_i]= \frac{1}{n}\sum \mu = \frac{1}{n} n \mu = \mu \end{aligned}\)

표본평균의 기댓값은 모평균이 되는 것을 볼 수 있습니다. 이를 통해, 모평균을 추정하려면 표본들의 평균값을 사용하는 것이 타당한 것을 알 수 있는 것이죠.

이제, 이를 신뢰구간이라는 개념으로 확장시켜 봅시다.

모평균을 추정하기 위해, 하나의 값인 (점추정량) 표본평균을 구했습니다.

중심극한 정리에 의해 표본평균은 평균이 \(\mu\) 이고, 분산이 \(\sigma^2 / n\) 인 정규분포를 따르게 됩니다. (따르게 된다고 가정됩니다.)

자연스럽게 표준화를 시킨 확률변수 \(\begin{aligned} Z = \frac{\bar{X} - \mu}{\sigma/ \sqrt{n}}\end{aligned}\) 는 평균이 0이고 분산이 1인 표준정규분포를 따르게 되죠.

지금까지 한 것은 불편추정량이라서 모평균의 추정량으로 사용한 표본평균을 중심극한 정리를 적용하여 표준정규분포를 따르는 확률변수로 변환시킨 것입니다.

이제 그 추정량이 어떤 확률분포를 가지는가를 알아냈으니, 범위에 따른 확률을 당연히 이 확률분포에 대입해 구할 수 있겠죠. 밑의 예처럼 말이죠.

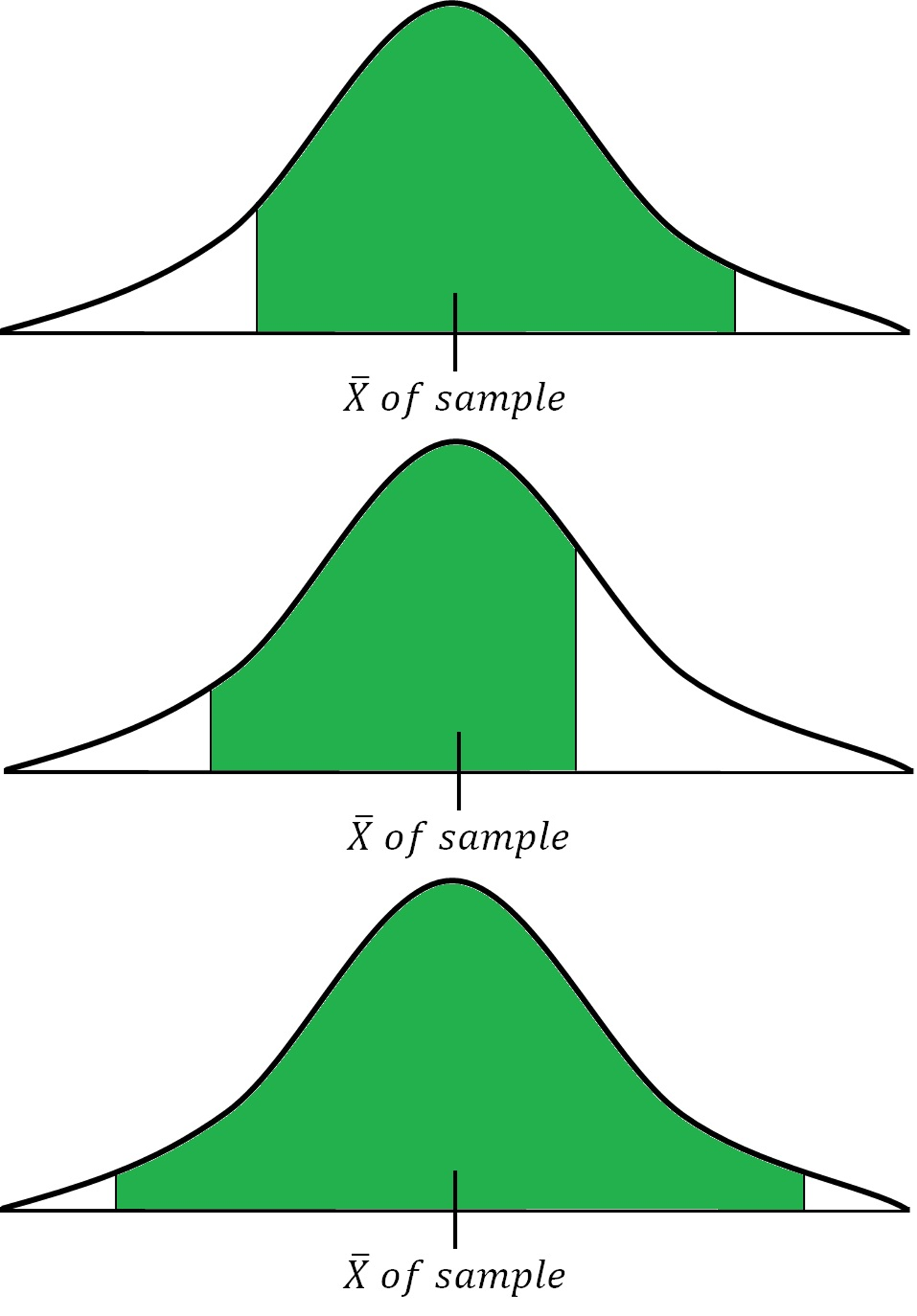
표본평균 자체가 불편 추정량임으로 일반적으로 표본평균값을 중심으로 대칭인 형태의 구간으로 확률을 구하게 되며, 똑같은 말을 반대로 하면, 확률을 정하면 => 구간을 정할 수 있게 되는거죠.

이것이 신뢰 구간입니다.

이제, 검정에 대해서 보죠.

먼저 검정을 하려면 검정할게 있어야 겠죠.

이전 chapter에서 살펴봤지만, 그것을 귀무가설이라고 하며, 사실상 귀무가설은 확률분포를 가정하는 것과 다르지 않습니다.

\(\begin{aligned} H_0 : \mu = \mu_0 \end{aligned}\)

위 처럼 귀무 가설을 정해봅시다. 모평균은 \(\mu_0\)라는 가설이죠.
다시 중심극한 정리를 생각해 볼 때, 모평균의 불편추정량인 표본평균은 정규분포를 따르게 되죠. 이 말인 즉슨, 평균 \(\mu_0\)을 중심으로 하고, 분산이 \(\sigma^2/n\)인 분포를 통해 검증하겠다는 말이며, 사실 확률분포를 가정한 것과 다름없어 지는 것이죠.

대립가설은 귀무가설과 상반되는 \(\begin{aligned} H_1 : \mu \ne \mu_0 \end{aligned}\) 가 될 것입니다.

이제 표본으로부터 표본평균을 구한 값(표본평균이 모평균의 불편추정량을 구하는 확률변수이기 때문입니다.)을 검정 통계량이라고 하며, 가정한 확률분포에서 표본으로부터 구한 검정통계량과 기각역을 비교하게 됩니다.

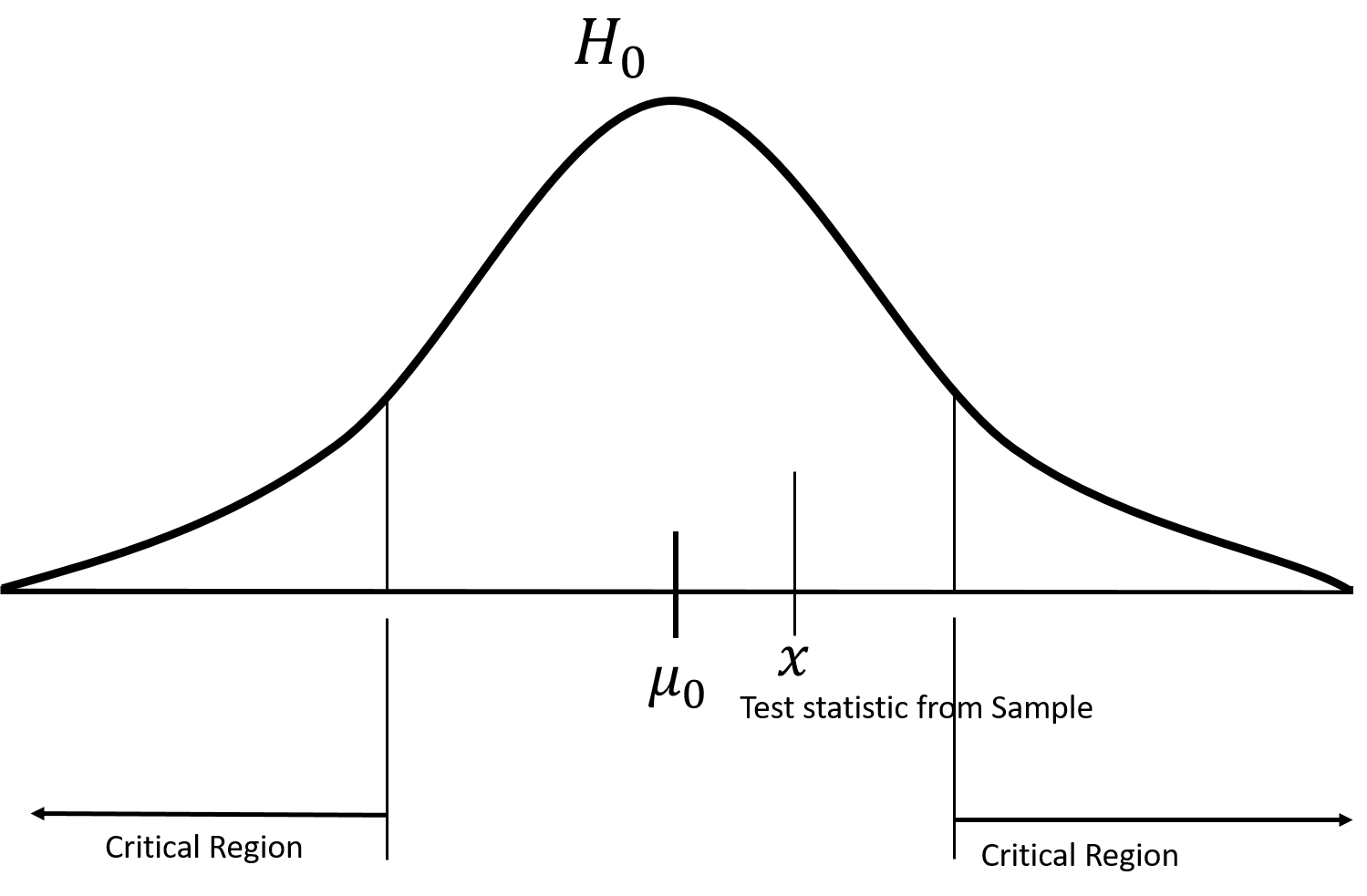
위와 같은 가정을 통해, 기각역에 검정통계량이 있으면 귀무가설을 기각한다. 그리고, 기각역에 속하지 않으면 귀무가설을 기각 할 수 없다. 라고 말할 수 있게 되는 것이죠.

모분산을 모르고 있을 때 단일 모평균의 추정 및 검정

모분산을 모를 때는 모평균을 어떻게 추정 및 검정해야 할까요?

먼저 모분산을 모른다는 말이 의미하는 것은, 확률평균이 따르게 될 정규분포의 분산을 구할 수 없다는 말입니다.

그러면, 다른 적절한 확률분포를 찾으면 될 것입니다. 그것이 student t-분포!가 되는 것이죠.

t-분포에 대해서 간단히 살펴보고 넘어갑시다.

\(\begin{aligned} t = \frac{\overline{X} - \mu}{S/\sqrt{n}} \end{aligned}\)

위와 같은 확률 변수를 가지면서,

\(\begin{aligned} g(t) &= \frac{\Gamma((\nu+1)2)}{\sqrt{\pi\nu}\Gamma(\nu/2)}(1+\frac{t^2}{\nu})^{-(\nu+1)/2} \end{aligned}\)

그리고 자유도가 \(\nu \space \space (\nu = n - 1 )\) 인 확률분포를 따르게 됩니다.

t 분포는 표본의 수 n가 커질 수록, 조금씩 정규분포에 가까워지는 형태를 가지고 있습니다.

왜 모분산을 모를 때, t-분포를 사용하는 것일까요?! 그 이유는, 당연하게도 모분산이 아닌 표본분산을 가지고 유도한 확률분포가 t-분포 이기 때문입니다.

신뢰구간의 추정 및 검정 방법은 귀무가설의 확률분포가 다르다는 것만 빼면, 모분산을 알아 정규분포를 사용한 경우와 동일합니다.