가설 검정 (Hypothetical Test)

통계적 가설은 하나 이상의 모집단에 대한 가정을 의미합니다.

보통, 모집단의 특성을 대표하는 숫자를 가정하게 되죠. (평균, 분산, 비율 등)

가설 검정을 왜 하는 것일까요?

바로 어떤 사실을 주장하거나, 특정 의견의 타당성을 확률적인 입장에서 검토하기 위한 것입니다.

가설 검정에서는 귀무 가설 (Null Hypothesis)과 대립 가설 (Alternative Hypothesis)이 존재합니다.

“귀무가설을 기각한다”, “귀무가설을 기각하지 못한다” 라고 검정에서는 얘기합니다. 보수적인 입장을 취한다고 생각하시면 쉬우실 것 같습니다. 확실히 이거다!라고 얘기할 수는 없다는 것이죠.

통계적인 가설 검정에서는 귀무가설이든 대립가설이든 가설을 세운다는 말은 특정한 확률분포를 가정한다는 말과 거의 동일합니다.

우리가 일반적으로 확률적으로 검증하기 위해 가정한 확률분포를 귀무가설이라고 생각하시면 나쁘진 않을 것 같습니다.

에러 (Error)

가설을 세운다는 말은 확률분포를 가정한다는 말과 동일하다고 했는데요.

확률 분포를 가정했으니, 뭔가 숫자를 얻어 낼 수 있게 됩니다.

검정에 사용되는 이 숫자를 검정 통계량 (test statistic)이라고도 합니다.

위에서 우리가 검증하게 될 확률분포가 귀무가설이라고 말씀드렸죠.

이 귀무가설, 즉 귀무가설 확률분포를 토대로 귀무가설을 기각할 확률과 기각하지 않을 확률을 계산해 낼 수 있습니다. (이것이 검정의 핵심이자 전부?!인가요?)

귀무 가설의 확률분포 (다른 말로 풀면, 귀무가설을 참이라 할 때)에서 기각하는 경우를 제 1종 과오 (type I error)라고 합니다. 이 1종 과오를 범할 확률을 \(\alpha\) 유의 수준 (level of significance)이라고 하구요.

유의 수준은 기각역 (Critical Region), 즉 어느 정도면 기각하겠다!라고 구간을 정하게 되면 구할 수 있게 됩니다.

같은 말을 반대로, 유의수준을 정한다는 말은 기각역을 정하겠다는 말이지요.

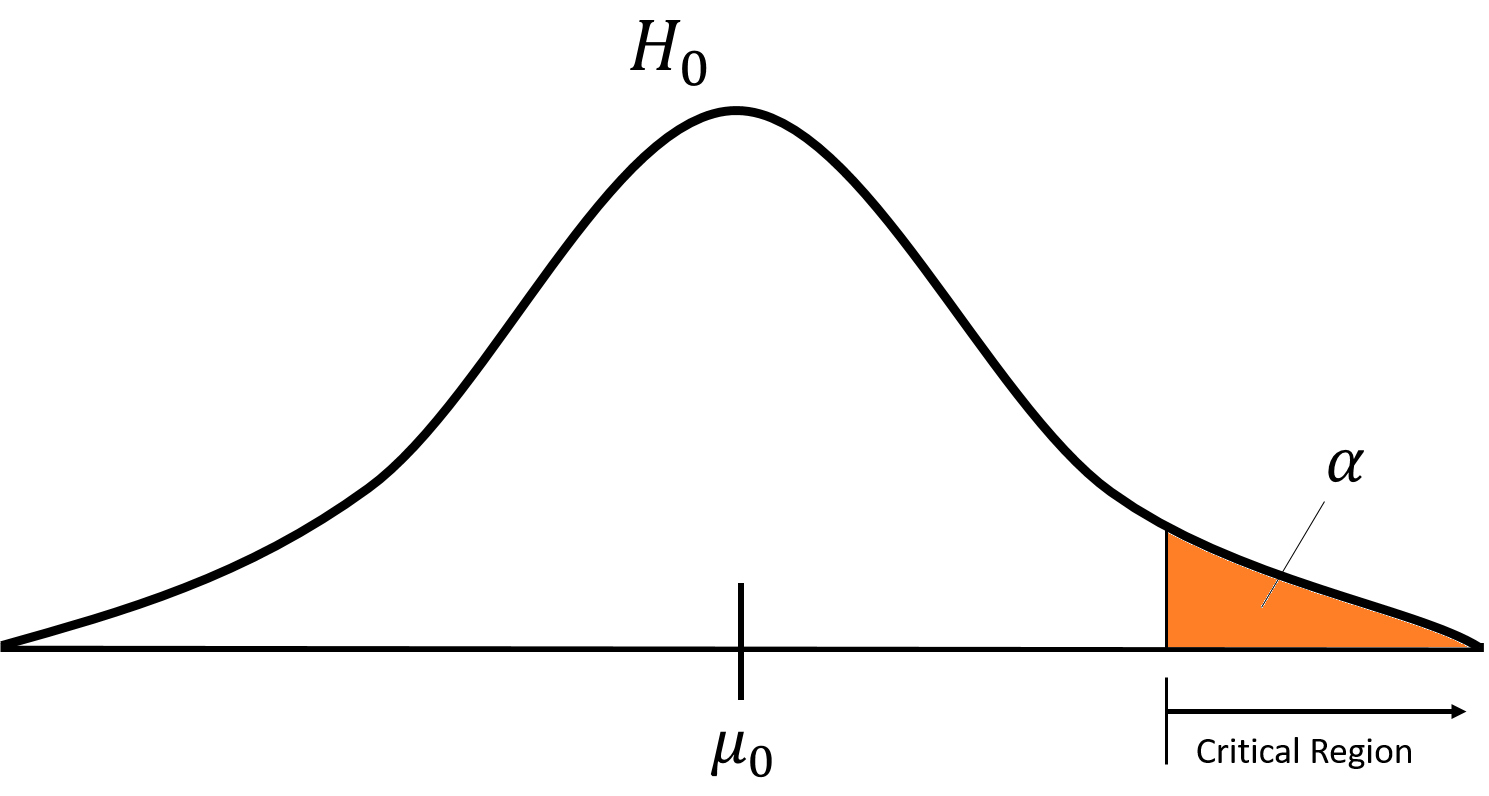
중간 정리를 하면, 귀무가설을 세운다는 말은 귀무가설 확률분포를 가정한다는 말과 다르지 않습니다. 어느 정도가 되면 귀무가설 확률분포를 따르지 않는다!라고 말할 수 있는 그 정도(기각역)를 정하면 이를 토대로 “귀무가설을 기각한다.” “기각하지 않는다!”라고 말할 수 있게 되는 것입니다.

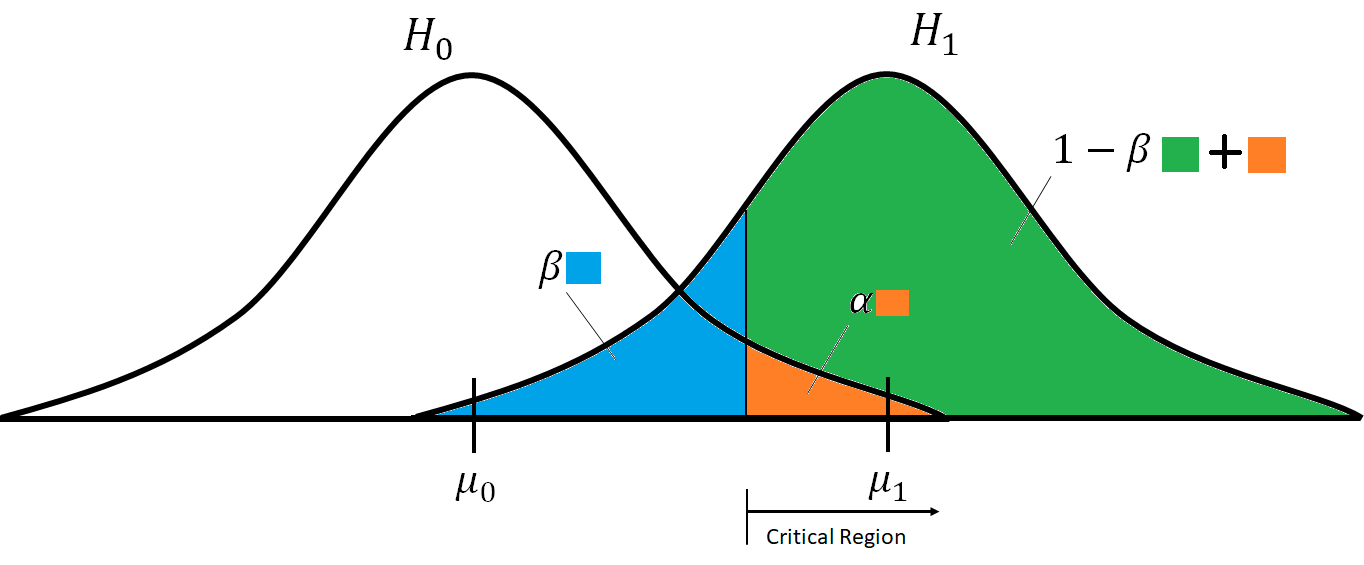
귀무가설 확률분포를 가정했으니, 대립가설 확률분포도 가정할 수 있겠죠?

귀무가설 확률분포에 이어, 대립가설 확률분포를 가정하면

대립가설 확률분포 입장에서 귀무가설 확률분포를 기각하지 않을 확률을 구할 수 있습니다. (다른 말로는, 대립가설이 참일 때, 귀무가설을 기각하지 않을 경우) 이 경우를 제 2종 과오 (type 2 error)라고 합니다.

그리고 제 2종 과오가 일어나지 않을 확률을 검정력 (power of test)라고 합니다. 제 2종 과오를 \(\beta\) 라고 하면, 검정력은 \(1-\beta\) 가 되는 것이죠.

귀무가설을 어떻게 세우는 건지 헤깔린다면 보통 등호관계로 세운다고 생각하시면 굉장히 편합니다.

어떤 값을 가정할 때, 그 값을 중심으로 분산을 띄는 특정한 확률분포를 가정하기가 자연스럽고 쉽기 때문입니다.

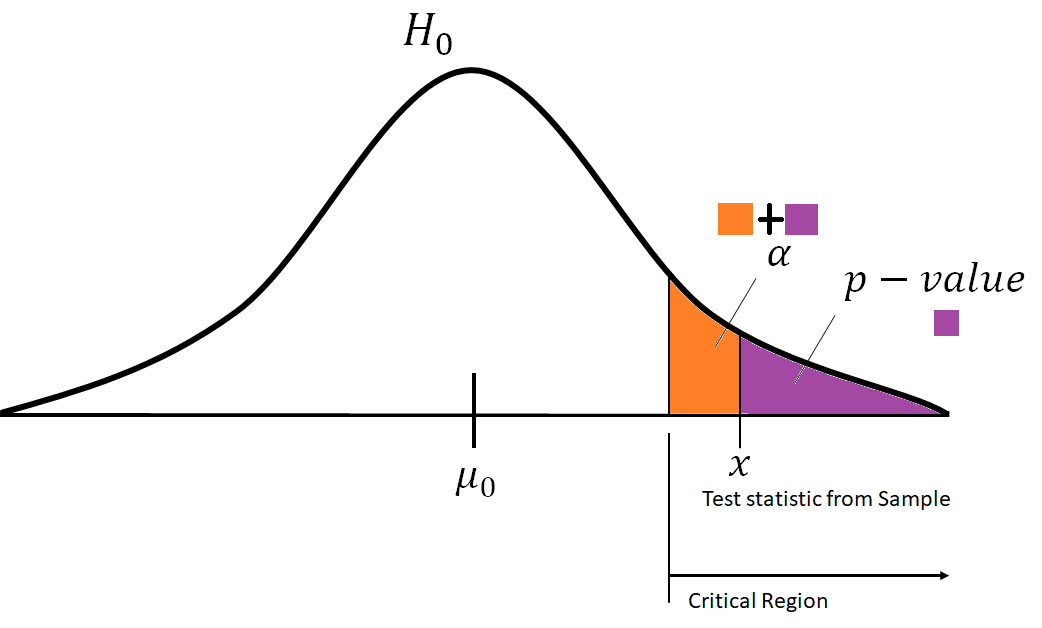
P-value

전통적으로 가설검정에서는 p-value가 많이 쓰이는데요.

일종의 유의수준 입니다. 단, 모집단에서 뽑은 표본에서 도출된 검정통계량(test statistic)이 유의하게 되는 경계가 되는 곳에서의 확률.

그 검정통계량 숫자에서 정한 유의수준을 p-value라고 합니다.

유의수준이 귀무가설을 기각할 확률(귀무가설 확률분포에서 벗어나려는 확률)이기에 p-value도 당연히 확률 값입니다.