배반과 독립

예전에 확률 사상의 배반과 독립의 관계는 항상 이해한 것 같다가도 다시 헤깔리는 귀찮은 녀석들이었습니다. 다시 한 번, 정리하면서 살펴보고 고민해보려 합니다.

배반 (Disjoint), 독립 (Independent)은 사상 (Events) 간의 관계에 대한 개념입니다.

결론부터 말하면, 사상 A와 사상 B가 있을 때,

배반은 \(A \cap B \subset \phi\),
독립은 \(P(A \cap B) = P(A)P(B)\)
을 만족하는 관계라고 말할 수 있습니다.

먼저, 배반에 대해서 살펴볼까요.

배반

사실 배반은 그리 어렵지 않은 개념입니다. 동시에 일어날 수 없는 사상 간의 관계를 말하며, 표본 공간 (Sampling Space)에서 사상 간의 교집합이 없는 것입니다.

밑의 그림과 같은 관계입니다.

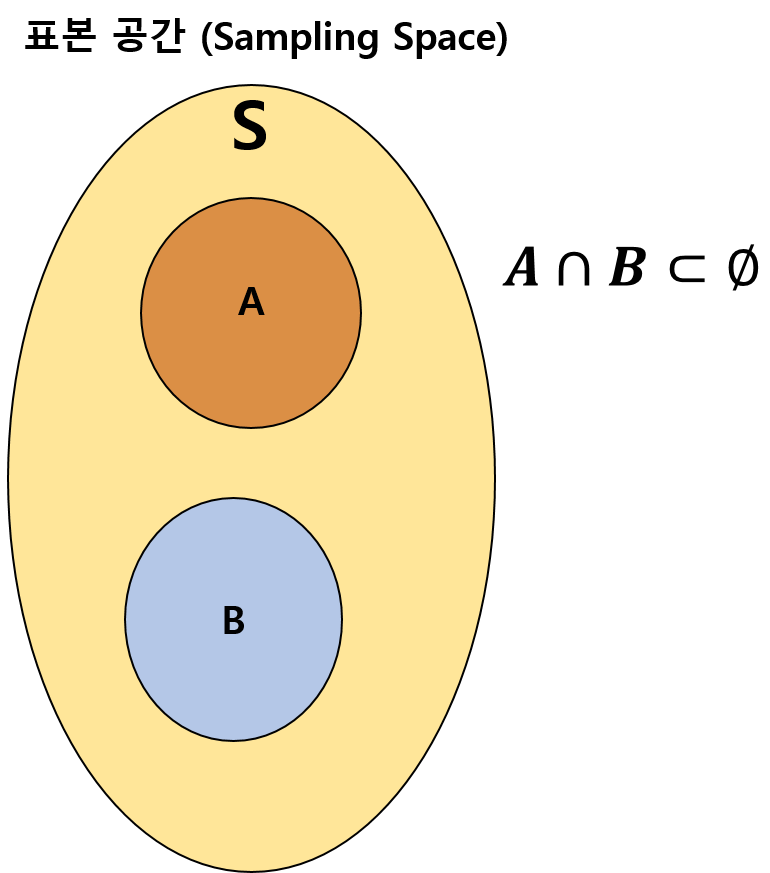
위 그림 처럼 표본공간에 임의의 사상 A와 사상 B가 있을 때,
\(P(A \cap B)\)와 \(P(A \cup B)\) 를 간단히 살펴보면,

먼저, 확률의 가법 정리(Additive Rule) 즉, 더하기 법칙은 아래와 같습니다. 사상안의 원소가 각각의 확률을 가지고 있다고 할 때, 일반적인 합집합의 연산과 동일한 것을 볼 수 있습니다.

\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]

\(A \cap B\) 는 사상 A 그리고 B 즉, A와 B를 동시에 만족하는 경우입니다.

배반의 정의에 따라 \(A \cap B = \phi\) 이며,

사상이 없는 확률은 0이기 때문에, \(P(A \cap B) = P(\phi) = 0\)이 되게 됩니다.

\(A \cup B\) 는 A 또는 B가 일어날 사상을 말합니다. 좀 더 풀어 말해서, A가 일어나든 B가 일어나든 A, B가 함께 포함되든 A, B 두 사상 중 한 개 이상을 만족하는 경우입니다.

이 경우의 확률은, 앞 서 \(P(A \cap B) = 0\) 이기에,

가법 정리를 따라, \(P(A \cup B) = P(A) + P(B)\) 이 되게 됩니다.

두 표본 공간의 결합 확률

조건부 확률과 독립에 대해 이야기를 나누기 전에, 먼저 아래 그림의 확률을 생각해보도록 하겠습니다.

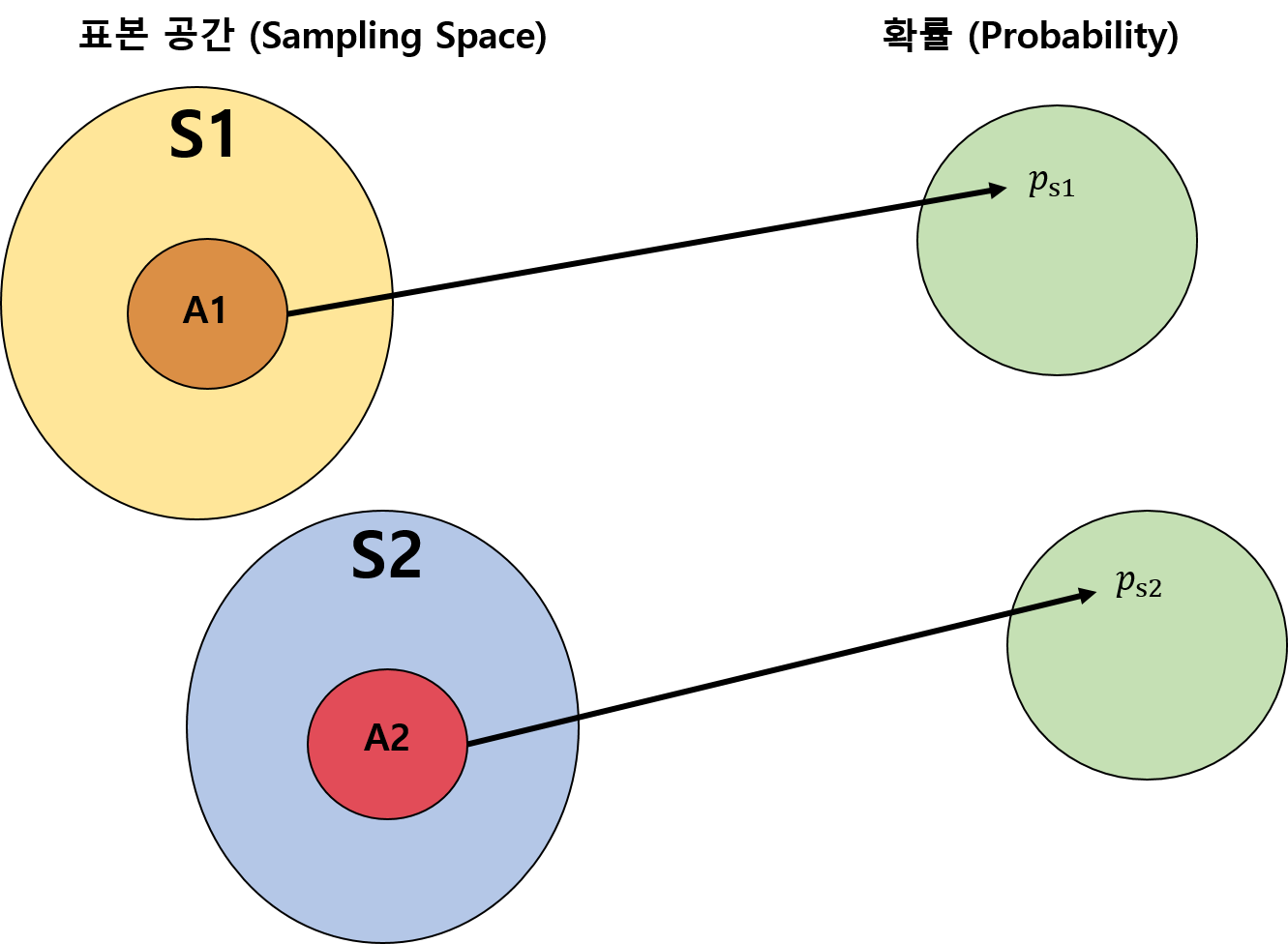
만약 서로 다른 표본 공간 S1과 S2에서 각각 사상 A1, A2가 함께 일어날 확률은 어떻게 표현할 수 있을까요?
(여기서 주의해야 할 점은 두 개의 표본 공간입니다. 하나의 표본공간이 아닙니다.)

\[P_{S1,S2}(A1, A2) = P_{S1}(A1) * P_{S2}(A2)\]

먼저, 위의 식과 같이 각각의 확률을 곱한 경우를 생각해 볼 수 있습니다.

(이 때, 표본 공간 S1과 S2에서 가중치(확률)를 매기는 방식이 다를 수 있지만,
S1, S2를 함께 다룰 때의 \(P_{S1,S2}\) 자체를 각각의 가중치 산정 방식으로 정해진 결합확률로 생각할 수 있습니다. 일종의 단위 Unit 처럼)

그렇다면, 이게 타당한 셈법일지, 좀 더 생각해보겠습니다.

표본 공간 S1에 속한 각각의 원소들의 확률을 아래와 같이 나타낸다면,
\(P_{S1}(A_i) = p_{S1}i\)

확률의 정의에 따라 다음식이 만족하게 됩니다.
\(\sum_{i \subset S1} p_{S1}i = 1\), \(0 <= p_{S1}i <= 1\)

마찬가지로 S2도 똑같이 나타낼 수 있습니다.
\(\sum_{i \subset S2} p_{S2}i = 1\), \(0 <= p_{S2}i <= 1\)

이제, S1의 원소로부터 모든 확률의 합과, S2의 원소로부터 모든 확률의 합을 곱해서 결합확률 \(P_{S1,S2}\) 를 생각해보겠습니다.

\(\begin{aligned} (\sum_{i}^{n}p_{S1}i)*(\sum_{j}^{m}p_{S2}j) &= p_{S1}1*p_{S2}1 + p_{S1}1*p_{S2}2 + p_{S1}1*p_{S2}3 + ... + p_{S1}n*p_{S2}m \\ &= P_{S1,S2}(1,1) + P_{S1,S2}(1,2) + P_{S1,S2}(1,3) + ... + P_{S1,S2}(n,m) \\ &= 1 \end{aligned}\)
\(p_{S1}\) 들의 합과 \(p_{S2}\) 들의 합이 각각 1이므로 이 합들을 곱했기 때문에 1이 되게 됩니다.

또, 중간에 나열한 항들을 살펴보면 모든 결합확률을 포함하고 있습니다.
자연스럽게 확률의 조건을 만족하게 되면서!

\(\sum_{i \subset S1}\sum_{j \subset S2}P_{S1,S2}(i,j) = 1, 0 <= P_{S1,S2}(i,j) <= 1\)

이렇게 서로 다른 표본공간의 결합확률이 단순한 곱의 형태가 확률의 정의를 만족하며 좋은 후보가 되는 것을 보였습니다.
이는 잠시 뒤에, 독립 관계를 이해하는데 큰 도움이 될 수 있으니 기억해두면 좋을 것 같습니다.

조건부 확률

다음은 조건부 확률에 대해서 생각해보겠습니다. 우리가 익숙한 조건부 확률 식을 먼저 보면,

\(P(A|B) = P(A \cap B)/P(B)\)
위와 같은 형태이고,

\(P(A|B)\) 는 사상 B가 일어났을 때, 사상 A가 일어날 확률입니다. 사실, 이 말도 잘 와닿지 않을 수 있습니다. 밑의 그림을 보면서 이어가도록 해보겠습니다.

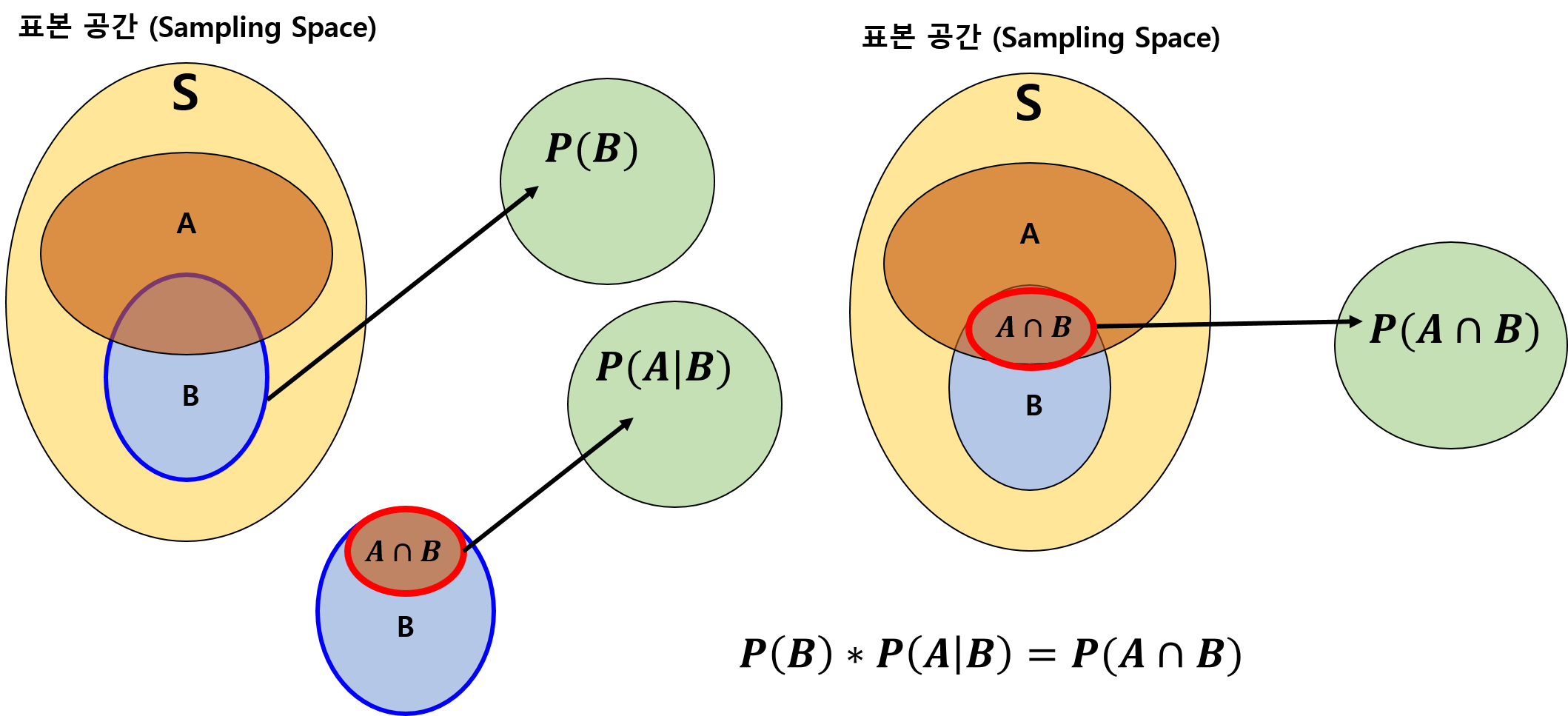
1. 표본 공간 S에서 사상 B가 일어나는 경우와
2. 표본 공간?! B 에서 A가 일어나는 경우를 함께 고려해보니
3. 결국 \(A \cap B\) 를 표본 공간 S에서 뽑은 셈이 됩니다. 이렇게 조건부 확률의 식을 생각할 수 있습니다.
   몇 가지만 더 살펴 보면,

\(P(A|B)\) 는 사상 B가 일어났을 때, 사상 A가 일어날 확률이라는 말에서
사상 B가 일어났을 때이 의미하는 것은, 표본 공간을 B로 줄인 상태에서 고려하겠다는 말입니다.
표본 공간을 줄인다는 말은, B에 속한 원속들이 가지는 확률의 값이 커진다는 말이 됩니다. (기존에는 더 큰 표본공간에서 사상 B는 아마 1보다 같거나 작은 확률을 가졌을테니, B로 새로운 표본공간을 구성하려면 B의 원소에 매칭되는 확률의 값이 커져야 합니다. 그 보정계수가 \(\frac{1}{P(B)}\) 가 되는 것입니다.

\(\begin{aligned} B = (b_1, b_2, ... b_k) \\ \\ P(B=b_1) + P(B=b_2) + ... + P(B=b_k) = P(B) \\ \\ \frac{P(B=b_1)}{P(B)} + \frac{P(B=b_2)}{P(B)} + ... + \frac{P(B=b_k)}{P(B)} = 1 \end{aligned}\)

더 재밌는 것은, 조건부 확률 식에 따라 생각해보면 단순한 사상 A가 일어날 확률을 다음처럼 표현할 수 있다는 것입니다.

\(P(A) = P(A|S)\)
즉, 표본공간 S가 발생했을 때 A가 일어날 확률!
( \(P(S) = 1\) , \(P(S \cap A) = P(A)\) 이므로 )

독립

드디어, 독립을 살펴볼 볼 때가 되었습니다!

사실, 독립의 좀 더 명확한 정의는 다음과 같습니다.

만약 사상 A와 B가 독립이라면,

\(P(A|B) = P(A)\) 가 되고, 반대도 마찬가지 입니다. \(P(B|A) = P(B)\)

말로 풀어서 생각해보면, B가 일어나든 말든 A는 동일한 가중치로 일어나게 된다는 말입니다.

조금만 생각해보면,
\(P(A \cap B) = P(A)P(B)\) 와 \(P(A|B) = P(A)\) 가 동일한 것인지 알 수 있습니다.

맨 처음의 독립을 나타내는 식( \(P(A \cap B) = P(A)P(B)\) )을 보고 문득 드는 생각은?!
두 표본공간의 결합확률이 떠올랐을 수 있을 것입니다.
그렇습니다. 사상이 독립이라는 말은 각각의 표본공간으로 나누어 생각할 수 있다는 말입니다.
이 어려운? 말은 마지막에 조금 더 설명을 보충해보려 합니다.


그렇다면, 위에서 \(P(A) = P(A|S)\) 는 어떻게 받아들일 수 있을까요? 표본공간 S와 그의 부분집합 A가 독립관계라니?!!

다시, 미궁속으로?!


일단, 식 자체는 정의와 일치하니 맞는 말인 것 같습니다. 이를 이해하기 위해 사상A와 B에 대한 독립관계식을 구체화하면,

\(P(A) = P(A|B) => P(A|S) = P(A|B)\)
표본공간 S에서의 A의 가중치나, 사상 B를 표본 공간으로 삼은데서 A의 가중치가 동일하다는 의미입니다.

다시 돌아와서,
\(P(A) = P(A|S) => P(A|S) = P(A|S)\)
풀어 말해서 표본공간 S에서 A의 가중치와 표본공간 S에서 A의 가중치는 같다?!
이제 당연하게 들릴 것입니다.

이 동일 가중치의 관계?!가 만족하려면, 두 개의 구별된 표본공간에 있는 각각의 확률변수를 생각하면 됩니다.

다른 말로는,

각 확률변수 X,Y,… 가 차원으로 (X, Y, ..) 나누어져 표본공간의 원소를 구성하고, Cartesian Product로 즉, 각각 원소의 곱으로 표현된 항이 모두 포함되어 있는 경우를 생각할 수 있습니다.

하나의 표본공간을 독립된 만큼 갯 수의 표본공간으로 분리한 뒤의 결합확률을 구하는 과정과 같다는 말입니다.

결론

고생이네요~!

정리해볼까요. 사상간의 관계를 표현하는 배반과 독립은 아래 그림과 같습니다.

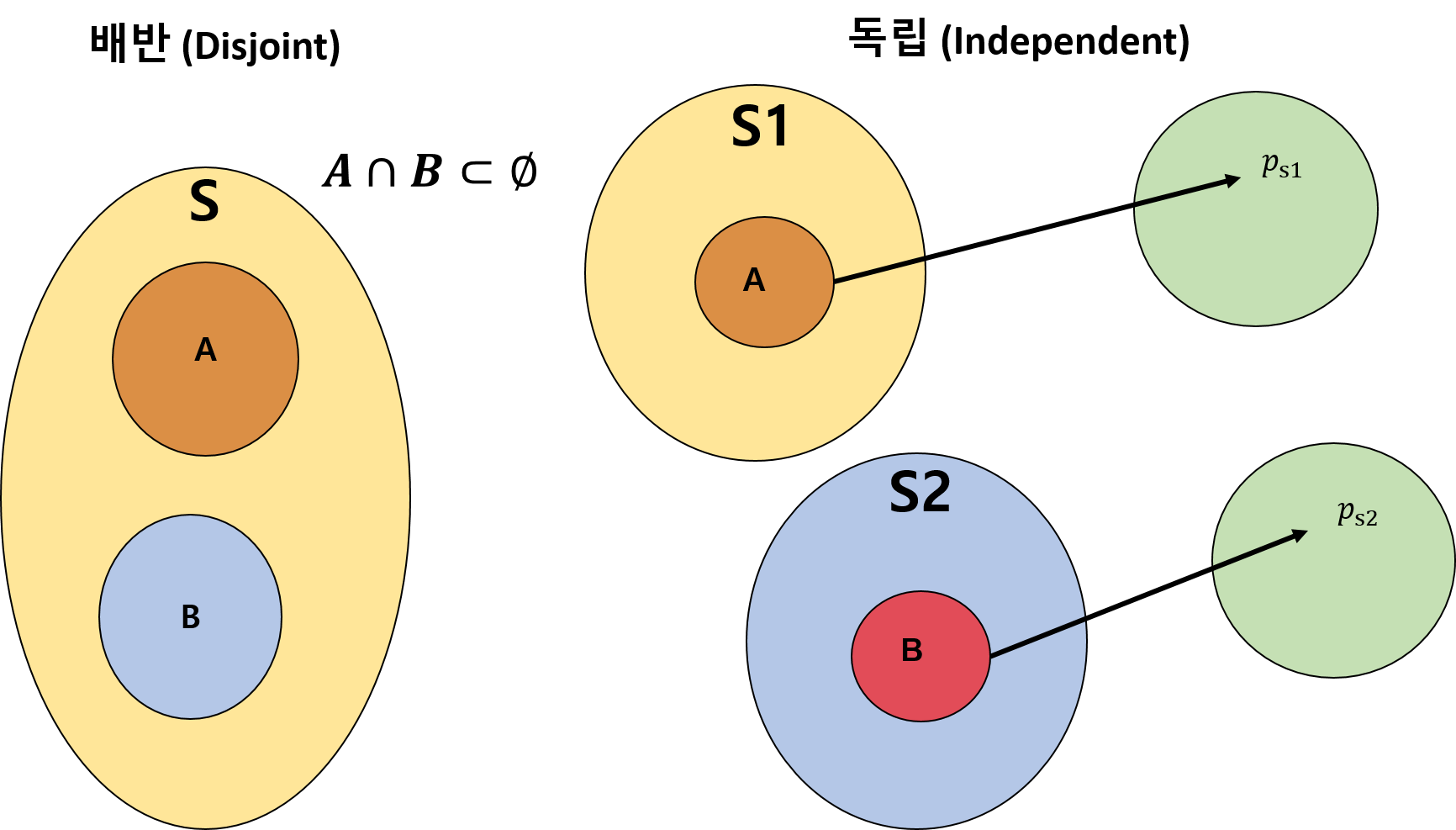
독립의 경우 => S = S1 X S2
where S : total Sampling Space

냠냠.