확률에 대해서 이야기를 하기 전에, 표본 공간과 사상을 먼저 이야기 할 필요가 있습니다.

I. 표본공간과 사상

표본공간 (Sample Space)은 쉽게 말해 특정한 일에 대해 모든 경우의 수를 담고 있는 집합입니다.

그리고, 사상 (Events)은 표본 공간의 부분집합을 의미하는 말입니다.

\(Events \subset Sample \space Space\)

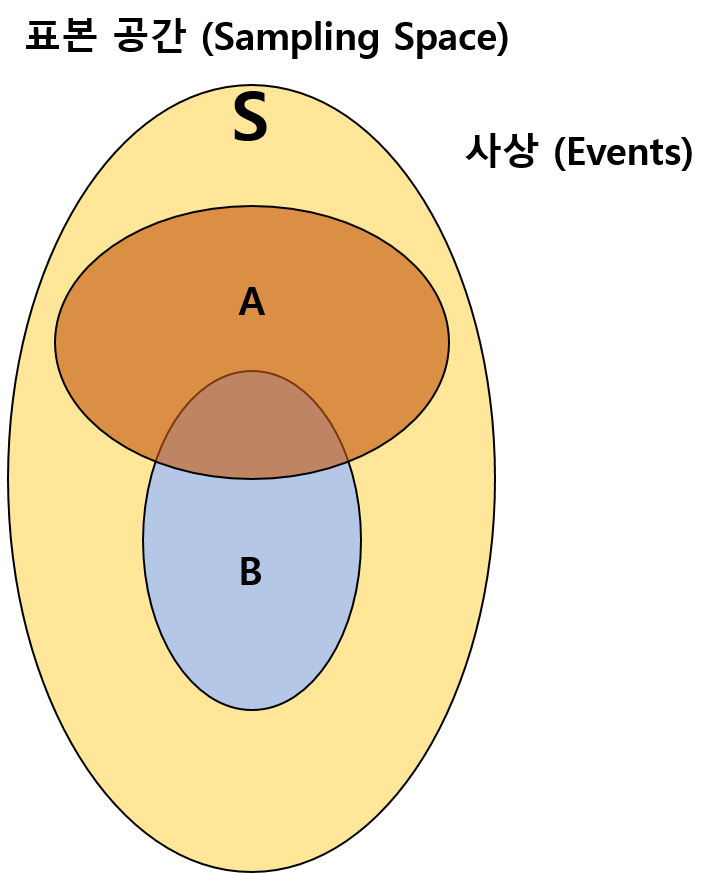
위 그림에서 S가 표본공간이라면, A, B는 사상이라고 볼 수 있습니다.

예시로 동전을 두 번 던져 앞뒷면이 나오는 경우를 따져본다면,
S = {(x,y)| x는 첫번째에 던진 동전의 경우, y는 두번째에 던진 동전의 경우}

이 때, 표본 공간은 S = { (앞,앞), (앞,뒤), (뒤,앞), (뒤,뒤) }가 됩니다.

사상 A를 첫번째 동전이 앞면, 두번째 동전이 뒷면이 나오는 경우라 하면 A = { (앞,뒤) }가 되고,
사상 B를 두번째 동전이 뒷면인 경우라 하면 B = { (앞,뒤), (뒤,뒤) }가 됩니다.

II. 확률과 확률변수

그렇다면, 확률은 무엇일까요?

표본 공간의 각 원소들이 가진 가중치(Weight)라고 생각할 수 있고 또는, 그냥 실수(R)라고 할 수 있습니다.

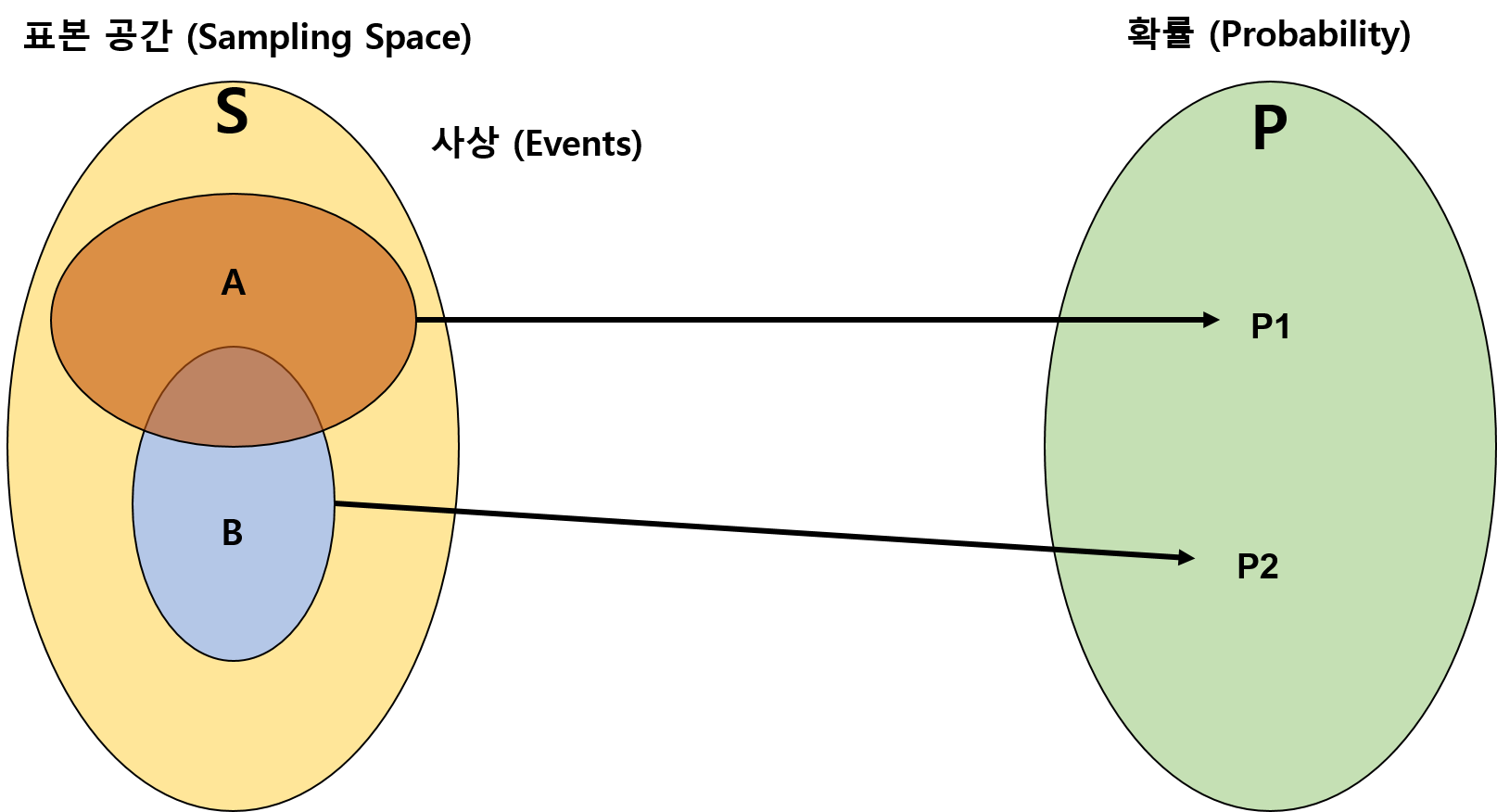
단, 만족해야하는 몇 가지 조건은,

표본 공간의 임의의 원소를 \(s_i\)라하고 이에 (연결, 맵핑, 혹은 부여)되는
(실수, 가중치)를 \(p_i\)라 할 때,

\(\Sigma p_i = 1 \space \space \space \space i:s_i \subset S\)
즉, 모든 확률의 합은 1이여야 한다는 것과,

\(0 <= p_i <= 1\)
각 확률은 0과 1사이의 값을 가져야 한다는 것이고,

\(P(\phi) = 0\)
공집합의 확률에 대해서는 0을 부여합니다. (사상이 없는 경우)

마지막으로 확률변수는 무엇일까요?
간단히 생각해, 표본 공간 속의 경우를 대표하고,
그 경우를 실수에 대응시킨 변수를 의미합니다.

보통 대문자로 가질 수 있는 모든 경우를 대표하고, 소문자로 특정한 값을 나타냅니다.

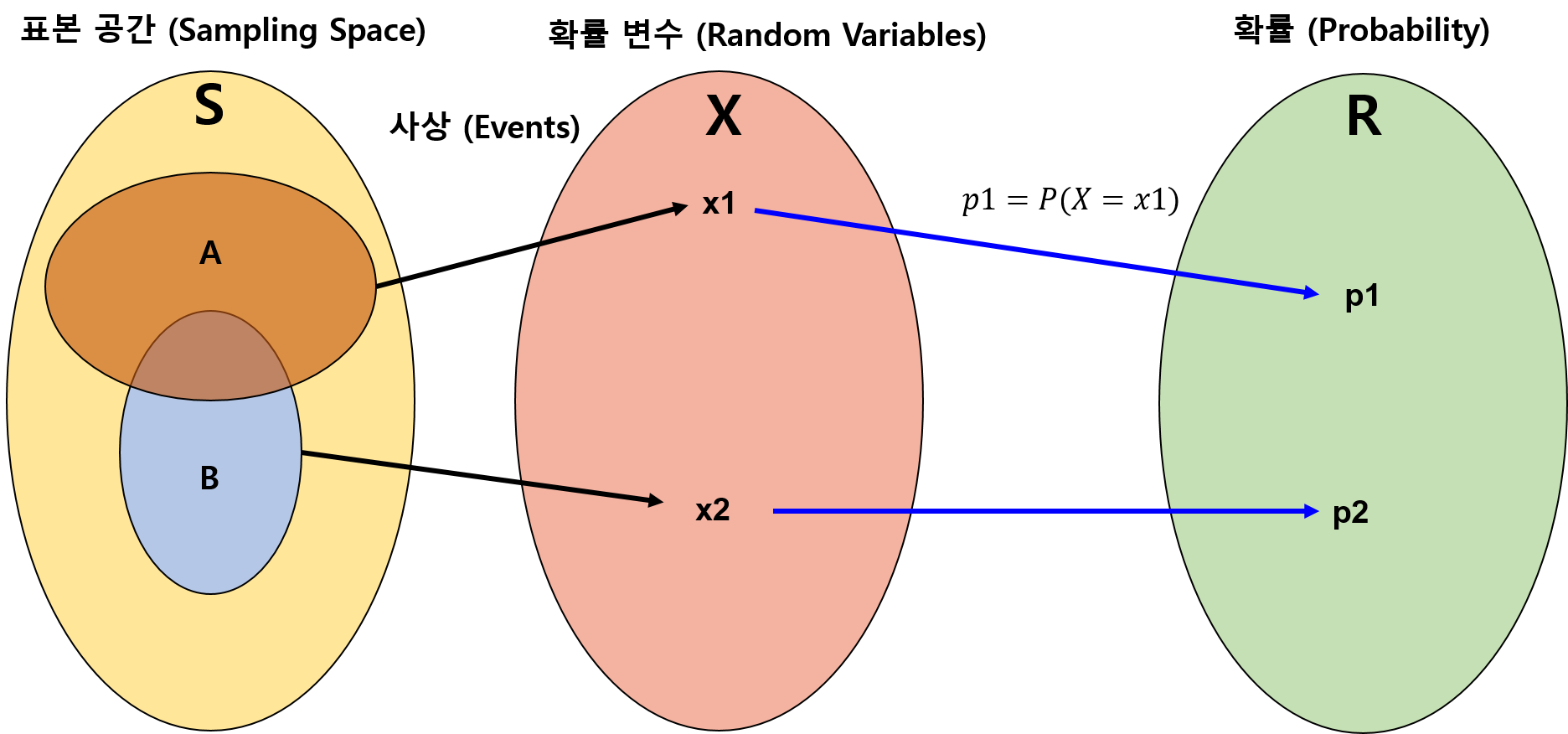
위의 그림을 정리해보면,
\(P(A) = p1 = P(X=x1)\)

많은 경우 표본 공간 자체를 확률변수로 삼기도 합니다. 예를 들어 키나 몸무게 등이 있을 수 있습니다.
만약 확률변수가 범주형(성별, 종류 등)인 경우에는 가변수 (Dummy Variables)를 사용해서 나타냅니다.
동전의 앞면을 1, 뒷면을 0이라 하는 것이 가변수의 한 예입니다.

표본공간은 형태에 따라 크게 2가지로 분류할 수 있습니다.

1. 이산표본공간

표본공간의 갯수가 유한하거나, 자연수에 대응하는 무한한(셀 수 있는) 원소로 이루어져 있을 때 “이산”표본공간 (Discrete Sample Space)이라 합니다.

이산표본공간에서
확률변수를 확률에 대응시켜 주는 \(P(X)\) 는 확률분포(Probability Distribution), 혹은 확률 질량함수(Probability Mass Function)라 합니다.

애초에 이렇게 구분하는 이유는, 표본공간의 형태에 따라 당연히 확률변수도 그에 맞는 적절한 형태를 가지기 때문입니다.

2. 연속표본공간

표본공간이 어떤 직선으로 대응시킬 수 있는 관계에 있으며 무한한 갯수를 가지고 있으면 “연속”표본공간(Continuous Sample Space)이라 합니다.

연속표본공간에서
\(P(X)\) 는 확률 밀도 함수 (Probability Density Function)이라고 합니다.

여기서 기억해야 하는 점은! 연속표본공간의 확률 밀도 함수의 값 자체는 확률이 아니라는 것입니다.

분포를 확률변수에 대해 그래프로 2차원에 그린다면, 넓이가 확률입니다.
좀 더 정확히 말해서, 확률변수의 범위가 산정되고 곱해져야 확률의 값을 가지게 됩니다.

이 말은 확률 밀도 함수 자체는 1보다 큰 값을 가질 수 있다는 말이겠지요.



일단 이쯤에서 간단히 넘어가 보도록 하겠습니다~!